Question

Using the equation


`√(x + 7) + 5 = x`
, are both x = 2 and x = 9 solutions or are one/both of them extraneous solutions? Explain.​

Answer 1

Given:

The equation is:

`√(x+7)+5=x`

To find:

Whether
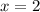`x=2` and
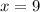`x=9` both are solutions or one/both of them extraneous solutions.

Solution:

We have,

`√(x+7)+5=x`

Subtract 5 from both sides.

`√(x+7)=x-5`

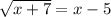
Taking square on both sides, we get

`x+7=(x-5)^2`

`x+7=x^2-10x+25`

`0=x^2-10x+25-x-7`

`0=x^2-11x+18`

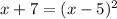
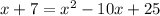
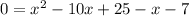
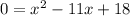
Splitting the middle term, we get

`x^2-2x-9x+18=0`

`x(x-2)-9(x-2)=0`

`(x-2)(x-9)=0`

`x=2,9`

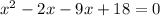
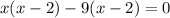
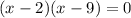
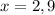
Now, substitute
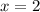`x=2` in the given equation.

`√(2+7)+5=2`

`√(9)+5=2`

`3+5=2`

`8=2`

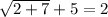
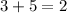
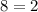
This statement is false because
`8\\eq 2`. So, 2 is an extraneous solution.

Substitute
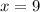`x=9` in the given equation.

`√(9+7)+5=9`

`√(16)+5=9`

`4+5=9`

`9=9`

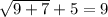
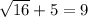
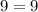
This statement is true. So, 9 is a solution of given equation.

Therefore, 2 is an extraneous solution and 9 is a solution of given equation.