Answer:
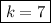
Explanation:
When interpreting this piecewise function, to determine whether or not the function is continuous, the limit to the left must be the same as the limit to the right.
Therefore to find an a value where the function is continuous at every point, we must determine where the limit is for the function.
In this case, the function is continuous at x = 7.
lim x→7 [x²] = lim x→7 [kx].
(7)² = k(7)
49 = 7k
÷7 ÷7
7 = k
k = 7.