Question

Find the second derivative of the function.

Answer 1

`\displaystyle d)\frac{d ^(2) y}{d{x}^(2) } = 2 + \frac{ 42}{ {x}^(4) }`

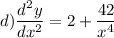
Explanation:

we would like to figure out the second derivative of the following:

`\displaystyle y = \frac{ {x}^(4) + 7}{ {x}^(2) }`

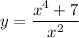
we can rewrite it thus rewrite:

`\displaystyle y = {x}^(2) + 7 {x}^( - 2)`

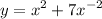
take derivative in both sides:

`\displaystyle (dy)/(dx) = (d)/(dx)( {x}^(2) + 7 {x}^( - 2) )`

by sum derivation we obtain:

`\displaystyle (dy)/(dx) = (d)/(dx){x}^(2) + (d)/(dx) 7 {x}^( - 2)`

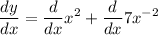
by exponent derivation we acquire:

`\displaystyle (dy)/(dx) = 2{x}^{} - 14 {x}^( - 3)`

take derivative In both sides once again:

`\displaystyle \frac{d ^(2) y}{d{x}^(2) } = (d)/(d x ) (2{x}^{} - 14 {x}^( - 3))`

use difference rule which yields:

`\displaystyle \frac{d ^(2) y}{d{x}^(2) } = (d)/(d x ) 2{x}^{} - (d)/(dx) 14{x}^( - 3)`

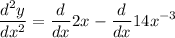
use exponent derivation which yields:

`\displaystyle \frac{d ^(2) y}{d{x}^(2) } = 2 + 42{x}^( - 4)`

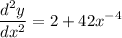
by law of exponent we get:

`\displaystyle \frac{d ^(2) y}{d{x}^(2) } = 2 + \frac{ 42}{ {x}^(4) }`

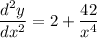
hence, our answer is d)