Answer:
See Explanation
Explanation:
Given
Edge Landscaping:

The rates (m) of the above table is calculated using:

From the table, we have the following points
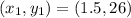

So, the rate is:
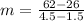
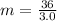
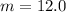
This means that the rate of edge landscaping is $12.0 per hour
The equation for Gatewood is not given. Hence, the rate cannot be calculated. However, the general procedure of calculating rates from a linear equation is as follows;
A linear equation is of the form:

Where:
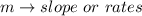
In other words, if the equation is:
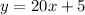
Then the rate is: 20 ($20/hour)
If the equation is:
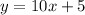
Then the rate is 10 ($10/hr)
Next, is to compare the rates;
For Edge landscaping, we have:
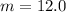
For Gatewood, we have:
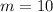 ------------ assume the equation is:
------------ assume the equation is:
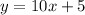
Compare the rates:
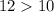
Hence, Edge landscaping has a greater hourly rate