Question

Unpolarized light of intensity 0.0288 W/m2 is incident on a single polarizing sheet. What is the rms value of the electric field component transmitted

Answer 1

the rms value of the electric field component transmitted is 3.295 V/m

Step-by-step explanation:

Given;

intensity of the unpolarized light, I = 0.0288 W/m²

For unpolarized light, the relationship between the amplitude electric field and intensity is given as;

`E_(max) = √(2\mu_0cI) \\\\E_(max) = \sqrt{2(4\pi * 10^(-7))(3* 10^8)(0.0288)} \\\\E_(max) = 4.66 \ V/m`

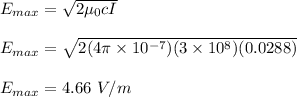
The relationship between the rms value of the electric field and the amplitude electric field is given as;

`E_(rms) = (E_0)/(√(2) ) =(E_(max))/(√(2) ) \\\\E_(rms) = (4.66)/(√(2) )\\\\E_(rms) = 3.295 \ V/m`

Therefore, the rms value of the electric field component transmitted is 3.295 V/m