Answer:
11.776
Step-by -step Step-by-step explanation:
Here we are given a equation which is ,
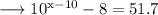
And we would like to solve this using logarithms , so firstly add 8 on both sides , we get ;

Simplify,
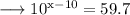
Now take log to the base 10 on both sides ,
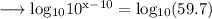
Recall that
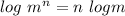 .So ;
.So ;
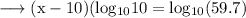
Again recall that
 .So ; here
.So ; here
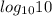 becomes 1 .
becomes 1 .
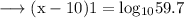
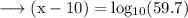
And the value of log 59.7 = 1.7759 . So on substituting this value , we have ;
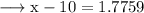
Add 10 to both sides ;

Simplify,

And we are done !


