Question

Solve using log. I have no idea how to use log so please explain how to use it.

Answer 1

Refer to picture with explanations on the right :)

Answer 2

11.776

Step-by -step Step-by-step explanation:

Here we are given a equation which is ,

`\rm\longrightarrow 10^(x-10)-8=51.7`

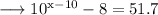
And we would like to solve this using logarithms , so firstly add 8 on both sides , we get ;

`\rm\longrightarrow 10^(x-10)= 51.7+8`

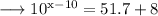
Simplify,

`\rm\longrightarrow 10^(x-10)= 59.7`

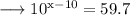
Now take log to the base 10 on both sides ,

`\rm\longrightarrow log_(10)10^(x-10)=log_(10)(59.7)`

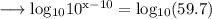
Recall that
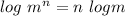`log\ m^n = n\ log m` .So ;

`\rm\longrightarrow (x-10)(log_(10)10=log_(10)(59.7)`

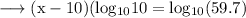
Again recall that
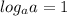`log_a a = 1` .So ; here
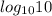`log_(10)10` becomes 1 .

`\rm\longrightarrow (x -10)1 = log_(10)59.7 \\`

`\rm\longrightarrow (x-10)= log_(10)(59.7)`

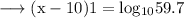
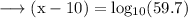
And the value of log 59.7 = 1.7759 . So on substituting this value , we have ;

`\rm\longrightarrow x -10 = 1.7759`

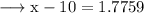
Add 10 to both sides ;

`\rm\longrightarrow x = 10+1.7759`

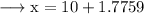
Simplify,

`\rm\longrightarrow \underline{\underline{\red{\rm { x = 11.7759 \approx 11.776}}}}`

And we are done !

`\rule{200}4`

`\large\red{\bigstar}\underline{\underline{\textsf{\textbf{ Some related formulae :- }}}}`

`\boxed{\boxed{\begin{minipage}{5cm}\displaystyle\circ\sf\ ^(a) log \ a= 1\\\\\circ \ ^(a)log \ 1 = 0 \\\\\circ \ ^{a ^(n)} log \ b^(m)= (m)/(n) *\:^(a)log \ b \\\\\circ \ ^{a^(m)} \ log \ b^(m) = \ ^(a)log \ b \\\\\circ \ ^(a)log \ b = (1)/(^(b)log \ a) \\\\\circ \ ^(a)log \ b = (^(m)log \ b)/(^(m) log \ a) \\\\\circ \ a^{^(a) logb} = b \\\\\circ \ ^(a)log \ b + ^(a)log \ c = \ ^(a)log(bc) \\\\\circ \ ^(a)log \ b -\: ^(a)log \ c = \ ^(a)log \left( (b)/(c) \right) \\\circ \ ^(a)log \ b \:\cdot\: ^(a)log \ c = \ ^(a)log \ c \\\\\circ \ ^(a)log \left( (b)/(c) \right) = \ ^(a)log \left((c)/(b)\right)\end{minipage}}}`