Question

Mr. K needs to hire an electrician. The electrician charges $82 for making a house call and an additional $55.00 per hour of labor. If Mr. K only budgeted $300 for the electrical repair, write, solve, and graph an inequality that shows the maximum amount of hours of labor Mr. K can afford to hire the electrician.

Answer 1

`\displaystyle4 \: \text{hours}`

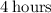
Explanation:

we are given that,

1. The electrician charges $82 for making a house call
2. an additional $55.00 per hour of labor
3. Mr. K only budgeted $300 for the electrical repair

let the hours be h

from the first condition we obtain:

`\displaystyle 82`

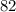
from the second condition we ge:

`\displaystyle 82+ 55h`

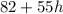
from the final condition we acquire:

`\displaystyle 82 + 55h \leqslant 300`

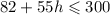
to figure out the hour we have to solve the equation to do so

cancel 82 from both sides:

`\displaystyle 55h \leqslant 215`

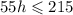
divide both sides by 55:

`\displaystyle h \leqslant 3.9636 \dots`

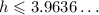
since 3.96.... is very close to 4 he can maximum afford 4 hours of labor

`\displaystyle h = 4`

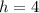
refer the attachment