Question

Coherent light with wavelength 603 nm passes through two very narrow slits, and the interference pattern is observed on a screen a distance of 3.00 m from the slits. The first-order bright fringe is a distance of 4.84 mm from the center of the central bright fringe.

Required:
For what wavelength of light will the first-order dark fringe (the first dark fringe next to a central maximum) be observed at this same point on the screen?

Answer 1

λ = 4.023 10⁻⁷ m

Step-by-step explanation:

The double-slit interference phenomenon is described by

d sin θ = (m + ½) λ destructive interference

d sin θ = m λ constructive interference

we can use trigonometry

tan θ = y / L

how these experiments occur for small angles

tan θ = sin θ/cos θ = sin θ

sin θ = y / L

we substitute

d y / L = (m + ½) λ destructive interference

d y / L = m λ constructive interference

with the expression for constructive interference we look for the separation of the slits

d = m λ L / y

d = 1 603 10⁻⁹ 3 /4.84 10⁻³

d = 3.738 10⁻⁴ m

Now let's analyze the case where the distance for constructive and destructive interference occurs at the same point y = 4.84 mm = 4.84 10⁻³m

d y / L = (m + ½) λ

λ =
`( d \ y)/(L\ (m+ 1/2) )`

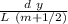
the first strip is for m = 1

let's calculate

λ =
`(3.738 \ 10^(-4) 4.84 \ 10^(-3) )/( 3 \ ( 1 + 0.5) )`

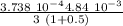
λ = 4.023 10⁻⁷ m