Answer: The number of milliliters of 654 mL for 0.587 M NaOH required to precipitate all of the
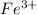 ions in 197 mL of 0.654 M
ions in 197 mL of 0.654 M
 solution as
solution as
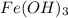 .
.
Step-by-step explanation:
The reaction equation is as follows.
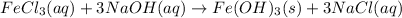
Therefore, moles of
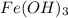 are calculated as follows.
are calculated as follows.
Moles = Molarity of
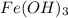
 Volume (in L)
Volume (in L)
= 0.654 M
 0.197 L
0.197 L
= 0.128 mol
Now, according to the given balanced equation 1 mole of
 reacts with 3 moles of NaOH(aq). Hence, moles of
reacts with 3 moles of NaOH(aq). Hence, moles of
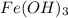 reacted are calculated as follows.
reacted are calculated as follows.
3
 0.128 mol = 0.384 moles of NaOH
0.128 mol = 0.384 moles of NaOH
As moles of NaOH present are as follows.
Moles of NaOH = Molarity of NaOH
 Volume (in L)
Volume (in L)
0.384 mol = 0.587 M
 Volume (in L)
Volume (in L)
Volume (in L) = 0.654 L (1 L = 1000 mL) = 654 mL
Thus, we can conclude that the number of milliliters of 654 mL for 0.587 M NaOH required to precipitate all of the
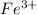 ions in 197 mL of 0.654 M
ions in 197 mL of 0.654 M
 solution as
solution as
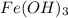 .
.