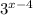Question

Consider the following. the parent function is f(x)=3^x.

partA- IF g(x)=f(x)+k whats the value of k?
part B- if h(x)=f(x+k) whats the values of k?
partC- write the function of G(x) and H(x)

Answer 1

Part A;

k = -1

Part B

k = -4

Part C

g(x) = 3ˣ - 1

h(x) =
`3^(x - 4)`

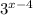
Step-by-step explanation:

The parent function of the graph, is f(x) = 3ˣ

Part A;

g(x) = f(x) + k

When x = 0, f(x) = 3⁰ = 1

g(x) = f(x) + k =
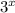`3 ^(x)` + k

Therefore;

When x = 0, g(0) = f(0) + k =
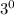`3 ^(0)` + k = k

From the graph, g(0) = -1, therefore;

g(0) = -1 = k

k = -1

Part B

h(x) = f(x + k)

When x = 4, h(4) = f(4 + k) =
`3 ^((4 + k))`

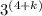
From the graph, h(4) = 1, therefore;

h(4) = 1 =
`3 ^((4 + k))`

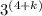
Therefore, we get;

ln(1) = (4 + k)·ln(3)

4 + k = ln(1)/ln(3) = 0

k = 0 - 4 = -4

k = -4

Part C

g(x) = f(x) + k

f(x) = 3ˣ, and k = -1

Therefore;

g(x) = 3ˣ - 1

h(x) = f(x + k)

f(x) = 3ˣ, and k = -4

Therefore;

h(x) =
`3^(x - 4)`