Question

The Quorum Company has a prospective 6-year project that requires initial fixed assets costing $962,000, annual fixed costs of $403,400, variable costs per unit of $123.60, a sales price per unit of $249, a discount rate of 14 percent, and a tax rate of 21 percent. What is the present value break-even point in units per year

Answer 1

5375

Step-by-step explanation:

Given that:

Initial Fixed assets costing = $962000

Annual fixed costs = $403400

Variable cost per unit = $123.60

Sales price per unit = $249.00

Discount rate = 14%

Tax rate = 21%

The contribution per unit = Sales price - Variable cost

= $(249.00 - 123.60)

= $125.40

The present value break-even point(BEP) is the region of sales level where the net present value (NPV) equals zero.

Assuming that the sales level = p

i.e.

NPV = PV(of inflows - of outflows)

Inflows = (p * contribution per unit - annual fixed cost)( 1- tax rate) + depreciation * tax rate

= (p * 125.4 - 403400) ( 1 - 0.21) + depreciation * tax rate

where;

depreciation = initial fixed assest cost/ lifetime of the project

= (125.4p - 403400)*0.79 + (962000/6)*0.21

= (125.4p - 403400)*0.79 + (160333.33)*0.21

= (125.4p - 403400)*0.79 + 33670

Now, the PV of the inflows =PV factor(6 years, 14%) * inflows

`= inflows * (( 1-(1.14)^(-6)))/(0.14)`

`= inflows * 3.8887`

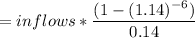
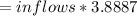
Replacing the value for inflows, we have:

`=((125.4p - 403400)*0.79 + 33670)* 3.8887`

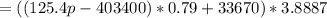
The PV of the outflows = Initial Fixed asset cost = $962000

∴

Equating both together using:

PV(of inflows - of outflows) = 0

((125.4p - 403400)*0.79 + 33670)* 3.8887 - 962000 = 0

((125.4p - 403400)*0.79 + 33670)* 3.8887 = 962000

(99.066p - 318686 + 33670) * 3.8887 = 962000

(99.066p - 285016) * 3.8887 = 962000

385.24p - 1108341.72 = 962000

385.24p= 962000 + 1108341.72

385.24p= 2070341.72

p = 2070341.72 / 385.24

p ≅ 5375