Answer:
See Explanation
Explanation:
The question is incomplete, as the 8 expressions are not given.
The general explanation is as follows
As complex as an expression may seem, you have to simplify each expression until it cannot be further simplified.
Then you categorize each result, depending on if it equals
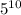 or not
or not
Take for instance:

Using law of indices:
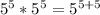
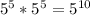 ---- equivalent
---- equivalent
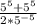
Factorize the numerator


Cancel out 2
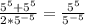
Apply law of indices
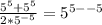
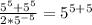
 ---equivalent
---equivalent

Express as exponent
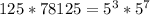
Apply law of indices
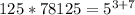
 ---- equivalent
---- equivalent
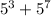
Solve exponents
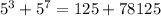
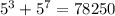 ---- not equivalent
---- not equivalent