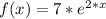Question

A curve passes through the point ( 0 , 7 ) (0,7) and has the property that the slope of the curve at every point P P is twice the y y -coordinate of P P . What is the equation of the curve

Answer 1

The equation for the curve is:

`f(x) = 7*e^(2*x)`

Explanation:

We know that for a curve defined as:

y = f(x)

The slope of the curve at the point x is:

y = f'(x)

where f'(x) = df(x)/dx

Here we know that we have a function that passes through the point (0, 7)

We also know that the slope of the curve at every point is twice the value of the y-coordinate. (remember that the y-coordinate is given by f(x))

Then we have two equations:

f(0) = 7

f'(x) = 2*f(x)

From the shape of the equation, we can assume than this is an exponential equation like:

`f(x) = A*e^(k*x)`

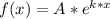
Replacing that in the second equation, we get:

`k*A*e^(k*x) = 2*A*e^(k*x)`

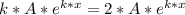
From that equation, we can conclude that k = 2

Then:

`f(x) = A*e^(2*x)`

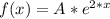
Now we can use the first equation:

f(0) = 7

With this, we can find the value of A.

`f(0) = 7 = A*e^(2*0)\\7 = A*e^0 = A*1\\7 = A`

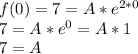
Then we can conclude that the equation for the curve is:

`f(x) = 7*e^(2*x)`