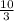Answer:
The sum converges at:
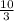
Explanation:
Given
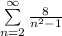
Express the denominator as difference of two squares
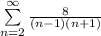
Express 8 as 4 * 2
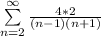
Rewrite as:
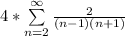
Express 2 as 1 + 1 + 0
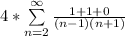
Express 0 as n - n
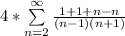
Rewrite as:
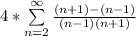
Split
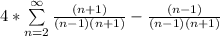
Cancel out like terms
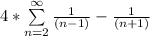
In the above statement, we have:
![a_3 + a_5 = 4[((1)/(2) - (1)/(4)) + ((1)/(4) - (1)/(6))]](https://img.qammunity.org/2022/formulas/mathematics/college/dm9118s9v3hp2o2n4dh2ewr46gfytqi9yy.png)
![a_3 + a_5 = 4[((1)/(2) - (1)/(6))]](https://img.qammunity.org/2022/formulas/mathematics/college/pel65kyy3tro8cknmx3rjn2v6sdri3r9e0.png)
Add
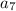
![a_3 + a_5 + a_7= 4[((1)/(2) - (1)/(6)) + ((1)/(7 - 1) - (1)/(7+1))]](https://img.qammunity.org/2022/formulas/mathematics/college/u4jh68c5l5dwl6afkkt1qeouz64qciuzyi.png)
![a_3 + a_5 + a_7= 4[((1)/(2) - (1)/(6)) + ((1)/(6) - (1)/(8))]](https://img.qammunity.org/2022/formulas/mathematics/college/zqih88qs6of84ithdjgatg6q6i59etny7x.png)
![a_3 + a_5 + a_7= 4[((1)/(2) - (1)/(8))]](https://img.qammunity.org/2022/formulas/mathematics/college/7vw2aituu60hs51fxaonw6kb5ypy6kcme0.png)
Notice that the pattern follows:
![a_3 + a_5 + a_7 + ...... + a_(k)= 4[((1)/(2) - (1)/(k+1))]](https://img.qammunity.org/2022/formulas/mathematics/college/nkdwqsekvvdvvduv6spw9h5ka4je13v0l9.png)
The above represent the odd sums (say S1)
For the even sums, we have:
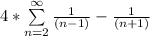
In the above statement, we have:
![a_4 + a_6 = 4[((1)/(3) - (1)/(5)) + ((1)/(5) - (1)/(7))]](https://img.qammunity.org/2022/formulas/mathematics/college/ps3awmv8nkku42123wg7k6tvgu62ur0ulq.png)
![a_4 + a_6 = 4[((1)/(3) - (1)/(7))]](https://img.qammunity.org/2022/formulas/mathematics/college/c4ksdnlod5u9w38sg0d0mqv0zutq8bd92c.png)
Add
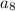 to both sides
to both sides
![a_4 + a_6 +a_8 = 4[((1)/(3) - (1)/(7)) + (1)/(7) - (1)/(9)]](https://img.qammunity.org/2022/formulas/mathematics/college/qf7cvb92z34cbnxezbdh2iu6kd9v5ze2tm.png)
![a_4 + a_6 +a_8 = 4[(1)/(3) - (1)/(9)]](https://img.qammunity.org/2022/formulas/mathematics/college/ozomhh8potzi6d27ylftwepebithkf8kh1.png)
Notice that the pattern follows:
![a_4 + a_6 + a_8 + ...... + a_(k)= 4[((1)/(3) - (1)/(k+1))]](https://img.qammunity.org/2022/formulas/mathematics/college/h0ollcmamcl7klb3mrsb3l6pgm9mz0us4e.png)
The above represent the even sums (say S2)
The total sum (S) is:
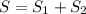
![S =4[((1)/(2) - (1)/(k+1))] + 4[((1)/(3) - (1)/(k+1))]](https://img.qammunity.org/2022/formulas/mathematics/college/ui04npblkhzcjnymxz61c15hh256ujrutb.png)
Remove all k terms
![S =4[((1)/(2)] + 4[((1)/(3)]](https://img.qammunity.org/2022/formulas/mathematics/college/vuwf7smpw3ioch00e0zzs958bu9p1q6lrg.png)
Open bracket
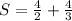
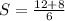
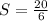
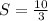
The sum converges at: