Question

A survey conducted by General Motors of 38 drivers in America, 34 indicated that they would prefer a car with a sunroof over one without. When estimating the proportion of all Americans who would prefer a car with a sunroof over one without with 99% confidence, what is the margin of error

Answer 1

The margin of error is of 0.1282 = 12.82%.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

The margin of error is of:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

A survey conducted by General Motors of 38 drivers in America, 34 indicated that they would prefer a car with a sunroof over one without.

This means that
`n = 38, \pi = (34)/(38) = 0.8947`

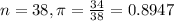
99% confidence level

So
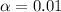`\alpha = 0.01`, z is the value of Z that has a p-value of
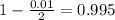`1 - (0.01)/(2) = 0.995`, so
`Z = 2.575`.

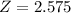What is the margin of error?

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`M = 2.575\sqrt{(0.8947*0.1053)/(38)} = 0.1282`

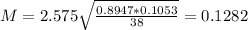
The margin of error is of 0.1282 = 12.82%.