Given:
In circle D,
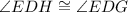 .
.
To find:
The length of JG.
Solution:
We know that, if two central angles are congruent then the corresponding chords are congruent and their measures are equal.
We have,
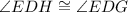
It means chords EH and EG are congruent and their measures are equal.
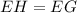
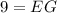
Using segment addition property, we get
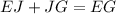
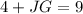
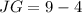
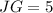
Therefore, the length of JG is 5 units.