Question

When 125 mL of 0.150 M Pb(NO3)2 is mixed with 145 mL of 0.200 M KBr, 4.92 g of PbBr2 is collected. Calculate the percent yield.

Answer 1

Y = 92.5 %

Step-by-step explanation:

Hello there!

In this case, since the reaction between lead (II) nitrate and potassium bromide is:

`Pb(NO_3)_2+2KBr\rightarrow PbBr_2+2KNO_3`

Exhibits a 1:2 mole ratio of the former to the later, we can calculate the moles of lead (II) bromide product to figure out the limiting reactant:

`0.125L*0.150(molPb(NO_3)_2)/(L) *(1molPbBr_2)/(1molPb(NO_3)_2) =0.01875molPbBr_2\\\\0.145L*0.200(molKBr)/(L) *(1molPbBr_2)/(2molKBr) =0.0145molPbBr_2`

Thus, the limiting reactant is the KBr as it yields the fewest moles of PbBr2 product. Afterwards, we calculate the mass of product by using its molar mass:

`0.0145molPbBr_2*(367.01gPbBr_2)/(1molPbBr_2) =5.32gPbBr_2`

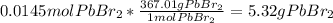
And the resulting percent yield:

`Y=(4.92g)/(5.32g) *100\%\\\\Y=92.5\%`

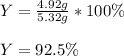
Regards!