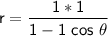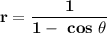Question

Find a polar equation of the conic in terms of r with its focus at the pole. Conic Eccentricity Directrix Parabola e = 1 x = −1

Answer 1

Explanation:

From the given information:

The Directrix x = - 1

The eccentricity e = 1

Since the Directrix x = - 1, it implies that the directrix appears on the left negative side of the pole and is vertical.

Hence, the conic equation in terms of r is:

`\mathsf{r =(ep)/(1-e \ cos \ \theta)}`

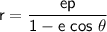
From the directrix to the pole, the distance p = 1

So;

`\mathsf{r =(1*1)/(1-1 \ cos \ \theta)}`

`\mathbf{r =(1)/(1- \ cos \ \theta)}`