Question

Given the statement 11^(n -6) is divisible by 5 for every positive integer n. What must be shown in the induction step?

Answer 1

Proved

Explanation:

The given data is:

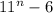`11^n - 6` not
`11^{n - 6`

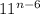
Required

Prove by induction that it is divisible by 5

Assume
`n = k`

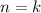
So, we have:

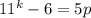`11^k - 6 = 5p` where p is a positive digit

Rewrite as:

`11^k = 5p + 6`

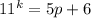
To solve further, we have to prove that
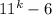`11^k - 6` is true for
`n=k+1`

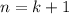
So, we have:

`11^(k+1) - 6`

`11^(k+1) - 6 = 11^k * 11 - 6`

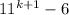
Add 0

`11^(k+1) - 6 = 11^k * 11 - 6 + 0`

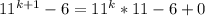
Replace 0 with
`-5 +5`

`11^(k+1) - 6 = 11^k * 11 - 6 - 5 + 5`

`11^(k+1) - 6 = 11^k * 11 - 11- 5`

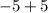
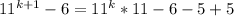
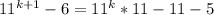
Factorize

`11^(k+1) - 6 = 11 (11^k - 1)- 5`

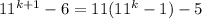
Substitute
`11^k = 5p + 6`

`11^(k+1) - 6 = 11 (5p + 6- 1)- 5`

`11^(k+1) - 6 = 11 (5p + 5)- 5`

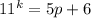
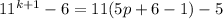
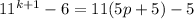
Factorize

`11^(k+1) - 6 = 11 *5(p + 1)- 5`

Factorize

`11^(k+1) - 6 = 5[11(p + 1)- 1]`

The 5 outside the bracket implies that it is divisible by 5