Answer:
35
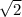
Explanation:
This scenario can be represented and solved by drawing a triangle. The hypotenuse of the triangle represents the ramp which has a length of 70 feet. The angle between the hypotenuse and the leg of the triangle that is parallel to the ground is 45 degrees. Since we know that this is a right triangle, we can conclude that this is a 45-45-90 degree right triangle. We can use the ratios of the sides of special right triangles to solve the problem from here. We know that the two sides and the hypotenuse of a 45-45-90 triangle can be represented as x, x, and x
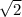 respectively. This means that the hypotenuse of 70 feet is equal to x
respectively. This means that the hypotenuse of 70 feet is equal to x
Then we solve the following equation:
x
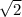 = 70
= 70
x =
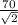
x =
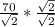
x =
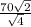
x =
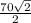
x =
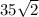
This means that each side of the triangle has a length of
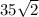 so that is also the height of the end of the ramp from the ground.
so that is also the height of the end of the ramp from the ground.