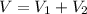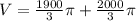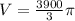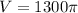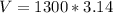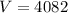Question

Plllzzz im new and i neeed help

find the volume of the following composite object. enter your answer as an integer in the box


​

Answer 1

4082

Explanation:

Given

The composite object

Required

The volume

The object is a mix of a cone and a hemisphere

Such that:

Cone

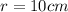`r = 10cm` ---- radius (r = 20/2)

`h = 19cm`

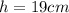
Hemisphere

`r=10cm`

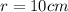
The volume of the cone is:

`V_1 = (1)/(3)\pi r^2h`

`V_1 = (1)/(3)\pi * 10^2 * 19`

`V_1 = (1900)/(3)\pi`

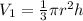
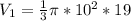
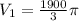
The volume of the hemisphere is:

`V_2 = (2)/(3)\pi r^3`

`V_2 = (2)/(3)\pi 10^3`

`V_2 = (2000)/(3)\pi`

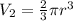
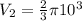
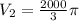
So, the volume of the object is:

`V = V_1 + V_2`

`V = (1900)/(3)\pi + (2000)/(3)\pi`

`V = (3900)/(3)\pi`

`V = 1300\pi`

`V = 1300 * 3.14`

`V = 4082`