Question

The table of values represents a polynomial function f(x).

How much greater is the average rate of change over the interval [5, 7] than the interval [2, 4] ?

x f(x)
2 230
3 638
4 1048
5 3452
6 4568
7 5002
8 6294
Enter your answer in the box.

Answer 1

366

Explanation:

I took the test lol

Answer 2

Given:

The table of values of the function f(x).

To find:

How much greater is the average rate of change over the interval [5, 7] than the interval [2, 4]?

Solution:

The average rate of change of a function f(x) over the interval [a,b] is:

`m=(f(b)-f(a))/(b-a)`

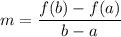
The average rate of change over the interval [5, 7] is:

`m_1=(f(7)-f(5))/(7-5)`

`m_1=(5002-3452)/(2)`

`m_1=(1550)/(2)`

`m_1=775`

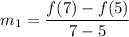
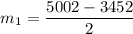
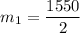
The average rate of change over the interval [2,4] is:

`m_2=(f(4)-f(2))/(4-2)`

`m_2=(1048-230)/(2)`

`m_2=(818)/(2)`

`m_2=409`

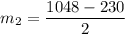
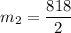
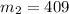
The difference between the average rate of change over the interval [5, 7] and the interval [2, 4] is:

`Difference=m_1-m_2`

`Difference=775-409`

`Difference=366`

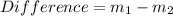
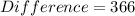
Therefore, the average rate of change over the interval [5, 7] is 366 more than the interval [2, 4].