Question

Factor 3x^3 - 15x^2 + 18x.

A. 3x(x - 2)(x - 3)
B. 3(x^2 + 2)(x-3)
C. 3x(x + 2)(x-3)
D. 3(x^2 - 2)(x-3)

Answer 1

The correct factorization of
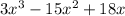`\(3x^3 - 15x^2 + 18x\)` is option C:
`\(3x(x + 2)(x - 3)\).`

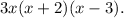
Step-by-step explanation:

To factor the given expression
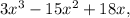`\(3x^3 - 15x^2 + 18x\),` we can start by factoring out the common factor, which is 3x. When we factor out 3x, we get:

`\[3x(x^2 - 5x + 6)\]`

Now, we need to factor the quadratic expression
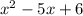`\(x^2 - 5x + 6\)`. This quadratic can be factored into
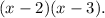`\((x - 2)(x - 3)\).` So, the complete factorization is:

`\[3x(x - 2)(x - 3)\]`

This matches with option C:
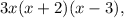`\(3x(x + 2)(x - 3)\),` confirming that option C is the correct factorization. Each factor corresponds to a root of the original polynomial, and when multiplied, they reconstruct the original expression. Therefore, option C accurately represents the factorization of
`\(3x^3 - 15x^2 + 18x\).`

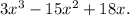
In conclusion, factorizing a polynomial involves identifying and factoring out common terms and then factoring any remaining quadratic expressions. The factorization provided in option C aligns with this process and correctly represents the given polynomial.

Answer 2

Step-by-step explanation:

3 x^3-15x^2+18x 3(x^3-5x^2+6x)