Question

Now suppose that bigger cups are ordered and the machine’s mean amount dispensed is set at μ=12. Assuming we can precisely adjust σ, what should we set σtobe so that the actual amount dispensed is between 11 and 13 ounces, 95% of the time?

Answer 1

σ should be adjusted at 0.5.

Explanation:

The Empirical Rule states that, for a normally distributed random variable:

Approximately 68% of the measures are within 1 standard deviation of the mean.

Approximately 95% of the measures are within 2 standard deviations of the mean.

Approximately 99.7% of the measures are within 3 standard deviations of the mean.

In this problem, we have that:

Mean 12.

Assuming we can precisely adjust σ, what should we set σtobe so that the actual amount dispensed is between 11 and 13 ounces, 95% of the time?

13 should be 2 standard deviations above the mean of 12, and 11 should be two standard deviations below the mean.

So 1 should be worth two standard deviations. Then

`2\sigma = 1`

`\sigma = (1)/(2)`

`\sigma = 0.5`

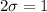
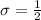
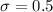
σ should be adjusted at 0.5.