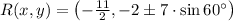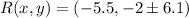Answer:
The possible coordinates for R are contained in the following expression:
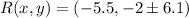
Step-by-step explanation:
From statement we notice that line segment PQ is parallel to x-axis and by Geometry we know that an equilateral triangles have three side with equal length and three angles of 60°. In consequence, the height of the triangle is parallel to the y-axis and the possible coordinates for point R are contained in this equation:
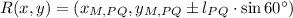 (1)
(1)
Where:
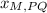 ,
,
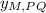 - Coordinates of the midpoint of the line segment PQ.
- Coordinates of the midpoint of the line segment PQ.
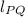 - Side length of the line segment PQ.
- Side length of the line segment PQ.
The length of the line segment PQ is determined by the Pythagorean Theorem:
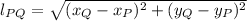 (2)
(2)
If we know that
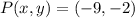 and
and
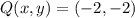 , then the length of the line segment PQ is:
, then the length of the line segment PQ is:
![l_(PQ) = \sqrt{[-2-(-9)]^(2)+[(-2)-(-2)]^(2)}](https://img.qammunity.org/2022/formulas/english/high-school/2zbmlhjacpejmtv6yc9rzx0zunfqak3f1y.png)
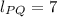
And the coordinates of the midpoint are, respectively:
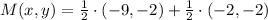
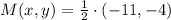
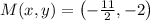
Lastly, the possible coordinates of vertex R are, respectively: