Answer:
a) Please find attached the required drawing of light passing through the lens
By the use of similar triangles;
The image distance from the lens = 26 cm
The height of the image = 14 cm
c) The image distance from the lens = 26 cm
The height of the image = 14 cm
Step-by-step explanation:
Question;
a) Determine the image distance and the height of the image
b) Calculate the image position and height
The given parameters are;
The height of the object, h = 14 cm
The distance of the object from the mirror, u = 26 cm
The focal length of the mirror, f = 13 cm
The location of the object = 2 × The focal length
Therefore, given that the center of curvature ≈ 2 × The focal length, we have;
The location of the object ≈ The center of curvature of the lens
The diagram of the object, lens and image created with MS Visio is attached
From the diagram, it can be observed, using similar triangles, that the image distance from the lens = The object distance from the lens = 26 m
The height of the image = The height of the object - 14 cm
b) The lens equation is used for finding the image distance from the lens as follows;

Where;
v = The image distance from the lens
We get;
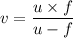
Therefore;
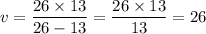
The distance of the image from the lens, v = 26 cm
The magnification, M =v/u
∴ M = 26/26 = 1, therefore, the object and the image are the same size
Therefore;
The height of the image = The height of the object = 14 cm.