Answer:
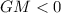
So the bouy does not float with its axis vertical
Step-by-step explanation:
From the question we are told that:
Diameter
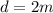
Length
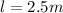
Weight
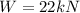
Specific weight of sea water
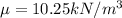
Generally the equation for weight of cylinder is mathematically given by
Weight of cylinder = buoyancy Force
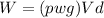
Where
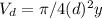
Therefore
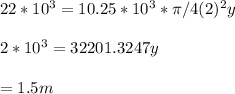
Therefore
Center of Bouyance B
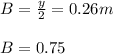
Center of Gravity

Generally the equation for\BM is mathematically given by
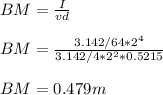
Therefore

Therefore
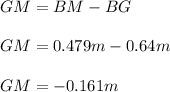
Therefore
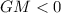
So the bouy does not float with its axis vertical