Question

Which point lies in the solution set of the inequality 1/2(x+2)+3y<8?

Answer 1

Note: Options are missing. So, the general solution of the given inequality is shown below.

Given:

The inequality is:

`(1)/(2)(x+2)+3y<8`

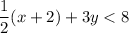
To find:

The point lies in the solution set of the given inequality.

Solution:

We have,

`(1)/(2)(x+2)+3y<8`

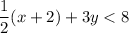
It can be written as:

`(1)/(2)(x)+(1)/(2)(2)+3y<8`

`(1)/(2)x+1+3y<8`

`(1)/(2)x+3y<8-1`

`(1)/(2)x+3y<7`

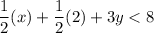
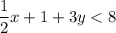
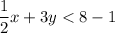
All the points that satisfy the above inequality are in the solution set of the given inequality.

For example (0,0).

`(1)/(2)(0)+3(0)<7`

`0<7`

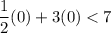
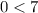
This statement is true. It means (0,0) is in the solution set.

For example (0,3).

`(1)/(2)(0)+3(3)<7`

`9<7`

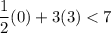
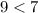
This statement is false. It means (0,3) is not in the solution set.

The graph of the inequality
`(1)/(2)x+3y<7` is shown below.

All the points in the shaded region are in the solution set but the points on the boundary line are not in the solution set.