Answer:
Explanation:
I'll just write log for log base 10. The important rules about logarithms we need to know are:
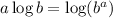
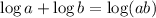
and at the end we'll need something like
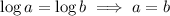
Suitably armed we can begin,
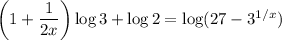
First rule,
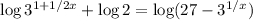
Second rule,
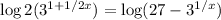
Third rule,
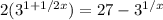
We can rewrite this to be a quadratic equation in
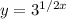 .
.
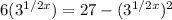
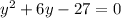
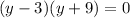
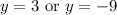
First solution:
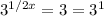
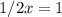
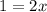
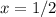
Second solution,

No real powers of 3 will be negative, no solution here.
Answer: x=1/2
Check:
1 + 1/2x = 2 so the left side is log 2(3²) = log 18
Right side, log(27-3^2) = log 18 √