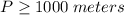Question

The length and breadth of a rectangular field are 312m and 186m respectively; correct to the nearest metres. Between what limits must the field's perimetre lie? (Write your final answer as an inequality)​

Answer 1

`P \geq 1000 \; meters`

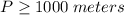
Explanation:

Given the following data;

Length = 312 meters

Breadth = 186 meters

To find the perimeter of the rectangle;

Mathematically, the perimeter of a rectangle is given by the formula;

Perimeter = 2(L + W)

Perimeter = 2(312 + 186)

Perimeter = 2(498)

Perimeter = 996 meters

To the nearest meters, we have;

Perimeter = 996 ≈ 1000 meters

Let P represent the perimeter of a rectangular field.

900 < P > 1000

Therefore,
`P \geq 1000 \; meters`