Question

PLEASE HELPP
64, 16, 4, 1 converging or diverging

Answer 1

The series 64, 16, 4, 1 is convergent.

Explanation:

Let be
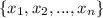`\{x_(1), x_(2),...,x_(n)\}` the set of values of the series. A series is convergent if and only if:

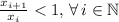`(x_(i + 1))/(x_(i)) < 1, \, \forall\,i\in \mathbb{N}` (1)

If we know that
`x_(1) = 64`,
`x_(2) = 16`,
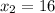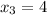`x_(3) = 4` and
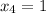`x_(4) = 1`, then the convergence ratio of each pair of consecutive values are, respectively:

`(x_(2))/(x_(1)) = (1)/(4)`,
`(x_(3))/(x_(2)) = (1)/(4)`,
`(x_(4))/(x_(3)) = (1)/(4)`

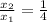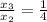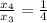
Hence, the series 64, 16, 4, 1 is convergent.