Given:
The function is
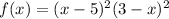
To find:
The derivative of the given function.
Solution:
Chain rule of differentiation:
![[f(g(x))]'=f'(g(x))g'(x)](https://img.qammunity.org/2022/formulas/mathematics/college/m7b4h3lgfqsxmsfpqykkv6etc1nwmzp4ue.png)
Product rule of differentiation:
![[f(x)g(x)]'=f(x)g'(x)+g(x)f'(x)](https://img.qammunity.org/2022/formulas/mathematics/college/89royu0ewgs5tw30gkeyn1thxgxdw8iqxc.png)
We have,
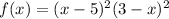
Differentiate with respect to x.
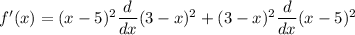
![f'(x)=(x-5)^2[2(3-x)(0-1)]+(3-x)^2[2(x-5)(1-0)]](https://img.qammunity.org/2022/formulas/mathematics/college/x0h90tesnpcxhebc2iu9jblshkhqlzed8u.png)
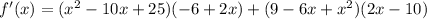
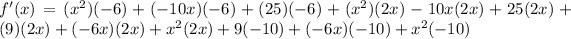
On further simplification, we get
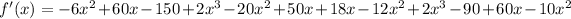
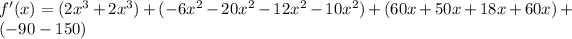
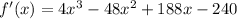
Therefore, the derivative of the given function is
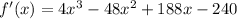 .
.