The height of tower B is approximately 68.47 meters, rounded to the nearest meter.
![\[ \text{Height of Tower B} \approx 68 \, \text{m} \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/4x0pj6gkwhyidgcb1qjcppnzmiw81ymdoz.png)
To find the height of tower B, we can use trigonometry. The tangent of the angle of elevation is the ratio of the opposite side (height of tower A) to the adjacent side (distance between towers A and B).
![\[ \tan(23^\circ) = \frac{\text{Height of Tower A}}{\text{Distance between Towers A and B}} \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/vnsuxyvvfbzelxetk9s445wi6ll2q5k9oy.png)
Let
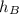 be the height of tower B, then:
be the height of tower B, then:
![\[ \tan(23^\circ) = (68)/(151) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/x1ym7s0oepo2zake2uszvwn3hw2rx16bf3.png)
Solving for
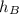 :
:
![\[ h_B = \tan(23^\circ) * \text{Distance between Towers A and B} + \text{Height of Tower A} \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/4ng5qvv2hk08a7b9loo9jsmrm27k0qj8vr.png)
![\[ h_B \approx \tan(23^\circ) * 151 + 68 \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/3gtc43afqcm0gc07m7q1k6q9axz3vcm1zv.png)
![\[ h_B \approx 68.47 \, \text{m} \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/8kgbly894het4kwrugmuohtgn7ohqp9300.png)