1 Answer

Piyin · Answer 1 · 2022-06-30T20:28:17+0000

Given:

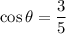
$\cos \theta =(3)/(5)$

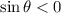
$\sin \theta <0$

To find:

The quadrant of the terminal side of
$\theta$ and find the value of
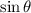$\sin\theta$ .

Solution:

We know that,

In Quadrant I, all trigonometric ratios are positive.

In Quadrant II: Only sin and cosec are positive.

In Quadrant III: Only tan and cot are positive.

In Quadrant IV: Only cos and sec are positive.

It is given that,

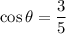
$\cos \theta =(3)/(5)$

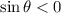
$\sin \theta <0$

Here cos is positive and sine is negative. So,
$\theta$ must be lies in Quadrant IV.

We know that,

$\sin^2\theta +\cos^2\theta =1$

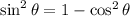
$\sin^2\theta=1-\cos^2\theta$

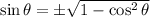
$\sin \theta=\pm √(1-\cos^2\theta)$

It is only negative because
$\theta$ lies in Quadrant IV. So,

$\sin \theta=-√(1-\cos^2\theta)$

After substituting
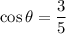$\cos \theta =(3)/(5)$ , we get

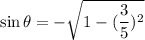
$\sin \theta=-\sqrt{1-((3)/(5))^2}$

$\sin \theta=-\sqrt{1-(9)/(25)}$

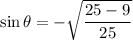
$\sin \theta=-\sqrt{(25-9)/(25)}$

$\sin \theta=-\sqrt{(16)/(25)}$

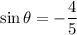
$\sin \theta=-(4)/(5)$

Therefore, the correct option is B.

Please log in or register to add a comment.