Question

Find a equation of a line that is perpendicular to y=-4x+3 and passes through the point (4,-1).

Answer 1

Given:

The given equation is:

`y=-4x+3`

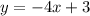
A line is perpendicular to the given line and passes through the point (4,-1).

To find:

The equation of required line.

Solution:

The slope intercept form of a line is:

`y=mx+b`

Where, m is slope and b is y-intercept.

We have,

`y=-4x+3`

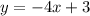
Here, the slope of the line is -4 and the y-intercept is 3.

Let the slope of required line be m.

We know that the product of slopes of two perpendicular lines is -1. So,

`m* (-4)=-1`

`m=(-1)/(-4)`

`m=(1)/(4)`

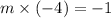
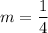
The slope of required line is
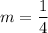`m=(1)/(4)` and it passes through the point (4,-1). So, the equation of the line is:

`y-(-1)=(1)/(4)(x-4)`

`y+1=(1)/(4)(x)-(4)/(4)`

`y=(1)/(4)x-1-1`

`y=(1)/(4)x-2`

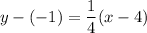
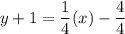
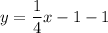
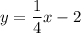
Therefore, the equation of the required line is
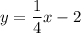`y=(1)/(4)x-2`.