Question

What is the perimeter of the quadrilateral ABCD?

Answer 1

Given:

The figure of a quadrilateral ABCD.

To find:

The perimeter of the quadrilateral ABCD.

Solution:

In an isosceles triangle, the two sides and base angles are congruent.

In triangle ABD,

`\angle DAB\cong \angle ABD` [Given]

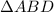`\Delta ABD` is an isosceles triangle [Base angle property]

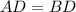`AD=BD` [By definition of isosceles triangles]

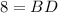`8=BD` ...(i)

In triangle BCD,

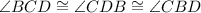`\angle BCD\cong \angle CDB\cong \angle CBD` [Given]

All interior angles of the triangle BCD are congruent, so the triangle BCD is an equilateral triangle and all sides of the triangle area equal.

`BC=CD=BD`

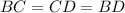
`BC=CD=8` [Using (i)] ...(ii)

Now, the perimeter of quadrilateral ABCD is:

`Perimeter=AB+BC+CD+AD`

`Perimeter=11+8+8+8`

`Perimeter=35`

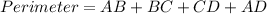
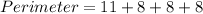
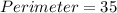
Therefore, the perimeter of the quadrilateral ABCD is 35 units.