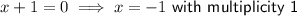Question

PLEASE HELP I'M BEGGING YOU SHOW STEPS IF YOU CAN

1.)Write -2x^3 (4x^3+5x^6) In Standard form, classify the degree and find the end behavior


2.) What Are The Zeros of the function and what are their multiplicities

f(x) =x^3+15x^2 +63x+49

Answer 1

Question 1

Given expression:

`-2x^3 (4x^3+5x^6)`

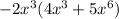
Apply the distributive law
`a(b+c)=ab+ac`:

`\implies -2x^3 \cdot4x^3+-2x^3 \cdot 5x^6`

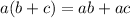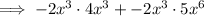
Multiply the numbers:

`\implies -8x^3 x^3-10x^3 x^6`

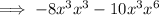
Apply exponent rule
`a^b \cdot a^c=a^(b+c)`

`\implies -8x^6-10x^9`

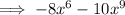
In standard form we write it in order from the greatest degree:

`\implies -10x^9-8x^6`

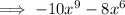
Therefore, as the polynomial is degree 9, it is a nonic polynomial.

End behaviors

As the leading coefficient is negative and the leading degree is odd:

`f(x) \rightarrow + \infty \textsf{, as } x \rightarrow - \infty`

`f(x) \rightarrow - \infty \textsf{, as } x \rightarrow + \infty`

----------------------------------------------------------------------------------------------

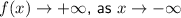
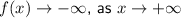
Question 2

Factor the given function to find the zeros

Given function:

`f(x) =x^3+15x^2 +63x+49`

`f(-1) =(-1)^3+15(-1)^2 +63(-1)+49=0`

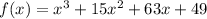
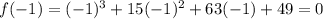
Therefore
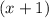`(x+1)` is a factor of the function

`\implies x^3+15x^2 +63x+49=(x+1)(x^2+bx+49)`

`=x^3+(b+1)x^2+(b+49)x+49`

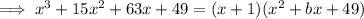
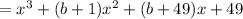
Comparing coefficients ⇒ b = 14

`\implies x^3+15x^2 +63x+49=(x+1)(x^2+14x+49)`

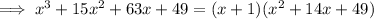
Factoring
`(x^2+14x+49)`:

`\implies (x^2+14x+49)=(x+7)(x+7)=(x+7)^2`

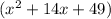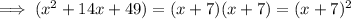
Therefore,

`f(x)=(x+1)(x+7)^2`

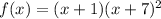
To find the zeros, equate to the function zero:

`(x+1)(x+7)^2=0`

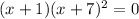
Therefore,

`x+1=0 \implies x=-1 \textsf{ with multiplicity 1}`

`x+7=0 \implies x=-7\textsf{ with multiplicity 2}`