Question

Question: Find the equation of the circle whose diameter is the segment between the intercepts of 3x + 4y = 24.

If you can answer this please explain the steps so I can understand, please and thank you so much!

Answer 1

`(x-4)^2+(y-3)^2=25`

Explanation:

We want to find the equation of a circle who diameter is the segment between the intercepts of the linear equation:

`3x+4y=24`

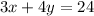
Find the intercepts first. To find the x-intercept, let y = 0:

`3x+4(0)=24\Rightarrow 3x=24\Rightarrow x=8`

The x-intercept is (8, 0).

To find the y-intercept, let x = 0:

`3(0) +4y=24\Rightarrow 4y=24\Rightarrow y=6`

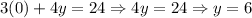
The y-intercept is (0, 6).

Since this segment is the diameter, its midpoint is our center.

Find the midpoint between (8, 0) and (0, 6). The midpoint formula is given by:

`\displaystyle M=\left((x_1+x_2)/(2), (y_1+y_2)/(2)\right)`

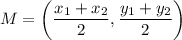
Hence, the center of the circle is:

`\displaystyle M=\left((8+0)/(2), (0+6)/(2)\right)=(4, 3)`

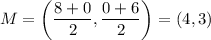
To find the radius of our circle, we can find the diameter and divide it by two.

The diameter is the length of the segment or the distance from (0, 6) to (8, 0).

Find the distance using the distance formula:

`d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

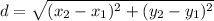
So, the diameter of our circle is:

`d=√((8-0)^2+(6-0)^2)=√(64+36)=√(100)=10`

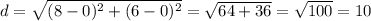
Therefore, the radius of our circle is 5.

The equation for a circle is given by:

`(x-h)^2+(y-k)^2=r^2`

Where (h, k) is the center and r is the radius.

Our center is (4, 3) and our radius is 5.

Therefore:

`(x-4)^2+(y-3)^2=25`