Question

The function P(t) = 4000(1.2) represents

the population of a small island
a. Does the function represent exponential
growth or decay?
b. what is the yearly percentage change in
population?
c. estimate how many people will be living on the island after 5 years.

Answer 1

Given:

Consider the given function is:

`P(t)=4000(1.2)^t`

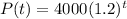
To find:

a. The type of exponential function (growth or decay).

b. Percentage change in population.

c. Population after 5 years.

Solution:

a. The general exponential function is:

`P(t)=P_0(1+r)^t` ...(i)

Where,
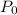`P_0` is the initial population and r is the rate of change in decimal.

If r<0, then the function represents exponential decay and if r>0, then the function represents exponential growth.

We have,

`P(t)=4000(1.2)^t`

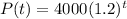
It can be written as:

`P(t)=4000(1+0.2)^t` ...(ii)

On comparing (i) and (ii), we get

`P_0=4000`

`r=0.2`

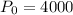
Since r>0, therefore the given function represents exponential growth.

b. From part (a), we have

`r=0.2`

So, the rate of change in the population is 0.2. Multiply is by 100 to get the percentage change in population.

`r\%=0.2* 100`

`r\%=20\%`

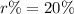
Therefore, the yearly percentage change in population is 20%.

c. We have,

`P(t)=4000(1.2)^t`

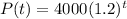
Substitute
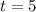`t=5` in the given function to find the population living on the island after 5 years.

`P(5)=4000(1.2)^5`

`P(5)=4000(2.48832)`

`P(5)=9953.28`

`P(5)\approx 9953`

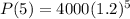
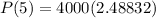
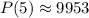
Therefore, the estimated population living on the island after 5 years is 9953.