Answer:
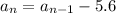 where
where
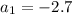
Explanation:
This is an arithmetic sequence with the first term is
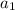 = -2.7 and has a common difference of
= -2.7 and has a common difference of
 .
.
Arithmetic Sequence:
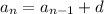
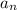 is the nth term and
is the nth term and
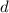 is the common difference.
is the common difference.
The common difference: -2.7, -8.3, -13.9...
Subtract: -2.7- (-8.3) = -5.6, -13.9 - (-8.3) = -5.6
Common difference:

Recursive rule:
