Question

HELP O_O
Find the Roots of the polynomial equation!!!

2x^3+2x^2-19x+20=0

Answer 1

Graph attached

Zeros are the x intercepts

• Only one real zero -1.047

Answer 2

Your given polynomial has only one real root which is x= -4

Explanation:

find any zero of the polynomial.

x-a divides the polynomial where a is a zero of polynomial:

So x+4 divides
`2x^(3) +2x^(2) -19x+20`

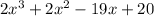
If we factor out a two, we can use the quadratic formula.

2(x^2-3x+2.5) so we have x = (-(-3)+/-(9-4*1*2.5)^(1/2))/2*1)=(3+i) or (3-i)/2 .

Final answer:

`2x^(3) +2x^(2) -19x+20=0`

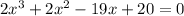
then x=-4, (3+i)/2, or (3-i)/2