Question

Please help! I think I have the equation set up.

Answer 1

`\bold{\huge{\underline{ Solution }}}`

Given :-

• Here, we have given one quadrilateral that is quadrilateral ABCD
• We also have given the angles of quadrilateral that is ( 6x + 5)° , ( 9x - 10)° , 80° and a right angle

To Find :-

Here, we have to find the value of x

Let's Begin :-

We have given quadrilateral ABCD here , whose angles are as follows

• Angle A = ( 6x + 5)°
• Angle B = ( 9x - 10)°
• Angle C = 80°
• Angle D = A right angled triangle

[ The measure of right angled triangle is 90° ]

We know that,

• Sum of the angles of quadrilateral is equal to 360°

That is

`\bold{\angle{ A + }}{\bold{\angle{B +}}}{\bold{\angle{C + }}}{\bold{\angle{D + = 360{\degree}}}}`

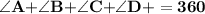
Subsitute the required values

`\sf{ ( 6x + 5){\degree} + 80{\degree}+ 90{\degree} + (9x - 10){\degree} = 360{\degree}}`

`\sf{ 6x + 5 + 170{\degree} + 9x - 10 = 360{\degree}}`

`\sf{ 15x - 5 = 360{\degree} - 170{\degree}}`

`\sf{ 15x - 5 = 190 {\degree}}`

`\sf{ 15x = 190 {\degree} + 5 }`

`\sf{ 15x = 195 {\degree}}`

`\sf{ x = }{\sf{( 195)/(15)}}`

`\sf{ x = }{\sf{\cancel{( 195)/(15)}}}`

`\bold{ x = 13 }`

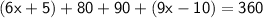
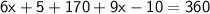
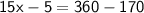
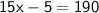
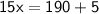
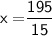
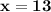
Hence, The value of x is 13 .

`\bold{\huge{\underline{\red{ Verification }}}}`

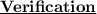
Measure of Angle A

`\sf{ = (6x + 5){\degree}}`

`\sf{ = (6(13) + 5 ){\degree}}`

`\sf{ = (78 + 5 ){\degree}}`

`\sf{ = 83{\degree}}`

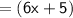
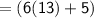
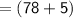
Measure of Angle D

`\sf{ = (9x - 10){\degree}}`

`\sf{ = (9(13) - 10){\degree}}`

`\sf{ = (117 - 10 ){\degree}}`

`\sf{ = 107{\degree}}`

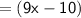
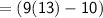
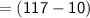
Now, we know that,

• Sum of angles of triangles is equal to 360°

That is,

`\sf{ 83{\degree} + 80{\degree}+ 90{\degree} + 107 {\degree} = 360{\degree}}`

`\sf{ 163{\degree}+ 90{\degree} + 107 {\degree} = 360{\degree}}`

`\sf{ 253{\degree}+ 107 {\degree} = 360{\degree}}`

`\sf{ 253{\degree}+ 107 {\degree} = 360{\degree}}`

`\bold{ 360{\degree} = 360{\degree}}`

`\bold{ LHS = RHS }`

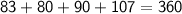
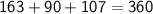
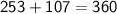
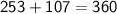
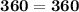
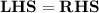
Hence, Proved.