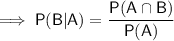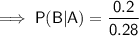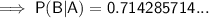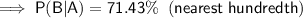Answer:
(a) 44.44%
(b) 71.43%
Explanation:
Let A = adults who visited a therapist.
Let B = adults who used antidepressants.
Therefore:
- P(A) = 0.28
- P(B) = 0.45
- P(A ∩ B) = 0.20
Part (a)

To calculate the probability that an adult visited a therapist (Event A) during the past year, given that he or she used antidepressants (Event B), use the conditional probability formula for A given B:
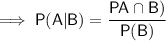
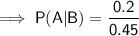

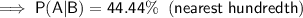
Part (b)

To calculate the probability that an adult used antidepressants (Event B), given that he or she visited a therapist (Event A) during the past year, use the conditional probability formula for B given A: