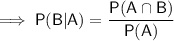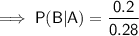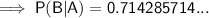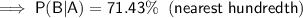Question

100 POINYS AND BRIANLIST

Answer 1

(a) 44.44%

(b) 71.43%

Explanation:

Let A = adults who visited a therapist.

Let B = adults who used antidepressants.

Therefore:

• P(A) = 0.28
• P(B) = 0.45
• P(A ∩ B) = 0.20

Part (a)

`\boxed{\begin{minipage}{5 cm}\underline{Conditional Probability formula}\\\\A given B:\\\\$\sf P(A|B)=(P(A \cap B))/(P(B))$\\\end{minipage}}`

To calculate the probability that an adult visited a therapist (Event A) during the past year, given that he or she used antidepressants (Event B), use the conditional probability formula for A given B:

`\implies \sf P(A | B)=(PA \cap B))/(P(B))`

`\implies \sf P(A | B)=(0.2)/(0.45)`

`\implies \sf P(A | B)=0.444444...`

`\implies \sf P(A | B)=44.44\%\;\; (nearest\; hundredth)`

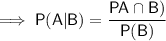
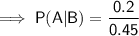
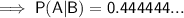
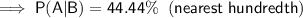
Part (b)

`\boxed{\begin{minipage}{5 cm}\underline{Conditional Probability formula}\\\\B given A:\\\\$\sf P(B|A)=(P(A \cap B))/(P(A))$\\\end{minipage}}`

To calculate the probability that an adult used antidepressants (Event B), given that he or she visited a therapist (Event A) during the past year, use the conditional probability formula for B given A:

`\implies \sf P(B | A)=(P(A \cap B))/(P(A))`

`\implies \sf P(B | A)=(0.2)/(0.28)`

`\implies \sf P(B | A)=0.714285714...`

`\implies \sf P(B | A)=71.43\%\;\; (nearest\; hundredth)`

Answer 2

Answer: See below

Explanation:

Let A represent an adult who visited a therapist

Let B represent an adult who used a non-prescription antidepressant

Given:
P(A) = 0.28 P

P (B) = 0.43

P(A Intersection B) = 0.22

a) P(B ∩ A) = P (B ∩ A) / P(A) = 0.22/0.27

P(B | A) = 0.79 or 79%

b) P(A ∩ B) = P (A ∩ B) / P(B) = 0.22/0.4.3

P(A | B) = 0.51 or 51%