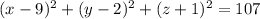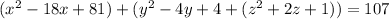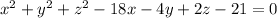Question

Find the equation of a sphere if one of its diameters has endpoints: (-14. -3, -6) and (-4, 7, 4) Note that you must move everything to the left hand side of the equation and that we desire the coefficients of the quadratic terms to be 1.

Answer 1

`x^2+y^2+z^2-18x-4y+2z-21=0`

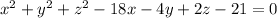
Explanation:

From the question we are told that:

Diameters has endpoints:
`(-14. -3, -6) & (-4, 7, 4)`

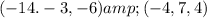
Generally the equation for Center of The sphere is mathematically given by

`C=((-14+(-4))/(2),(-3+(7))/(2),(-6+(4))/(2))`

`C=(9,2,-1)`

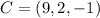
Generally the equation for Radius of the sphere is mathematically given by

`R=√((9-2)^2+(2-9)^2+(-1-2)^2)`

`R=√(107)`

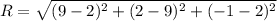
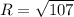
Therefore the Equation of the Sphere is

`(x-9)^2+(y-2)^2+(z+1)^2=107`

`(x^2-18x+81)+(y^2-4y+4+(z^2+2z+1))=107`

`x^2+y^2+z^2-18x-4y+2z-21=0`