Question

You are told that a random sample of 150 people from Manchester New Hampshire have been given cholesterol tests, and 60 of these people had levels over the "safe" count of 200. Construct a 95% confidence interval for the population proportion of people in New Hampshire with cholesterol levels over 200.

Answer 1

The 95% confidence interval for the population proportion of people in New Hampshire with cholesterol levels over 200 is (0.3216, 0.4784).

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

You are told that a random sample of 150 people from Manchester New Hampshire have been given cholesterol tests, and 60 of these people had levels over the "safe" count of 200.

This means that
`n = 150, \pi = (60)/(150) = 0.4`

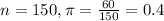
95% confidence level

So
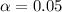`\alpha = 0.05`, z is the value of Z that has a p-value of
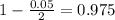`1 - (0.05)/(2) = 0.975`, so
`Z = 1.96`.

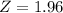The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.4 - 1.96\sqrt{(0.4*0.6)/(150)} = 0.3216`

The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.4 + 1.96\sqrt{(0.4*0.6)/(150)} = 0.4784`

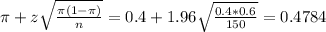
The 95% confidence interval for the population proportion of people in New Hampshire with cholesterol levels over 200 is (0.3216, 0.4784).