Question

A circle in the standard (x,y) coordinate plane has

center C(−1,2) and passes through A(2,6). Line
segment AB
___ is a diameter of this circle. What are the
coordinates of point B ?

Answer 1

Given:

Center of a circle is at point C(-1,2).

AB is the diameter of the circle.

Coordinates of the point A are A(2,6).

To find:

The coordinates of point B.

Solution:

Let the coordinates of point B are (a,b).

If AB is the diameter of the circle, then A and B are end points of diameter of the circle and the center C is the midpoint of AB.

`Midpoint=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

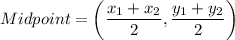
Point C = Midpoint of AB

`(-1,2)=\left((2+a)/(2),(6+b)/(2)\right)`

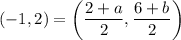
On comparing both sides, we get

`(2+a)/(2)=-1`

`2+a=-1* 2`

`a=-2-2`

`a=-4`

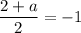
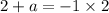
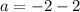
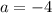
Similarly,

`(6+b)/(2)=2`

`6+b=2* 2`

`b=4-6`

`b=-2`

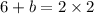
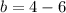
Therefore, the coordinates of point B are (-4,-2).