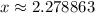Use Newton’s method to approximate the indicated root of the equation correct to six decimal places. The positive root of 3 sin x = x

Question

asked Dec 5, 2022 218k views

1 Answer

Robert Iver · Answer 1 · 2022-12-09T11:57:34+0000

Answer:

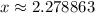
$x \approx 2.278863$

Explanation:

Required

The positive root of
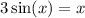
$3\sin(x) = x$

Equate to 0

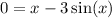
$0 = x -3\sin(x)$

So, we have our function to be:

$h(x) = x -3\sin(x)$

Differentiate the above function:

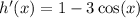
$h'(x) = 1 -3\cos(x)$

Using Newton's method of approximation, we have:

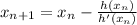
x_(n+1) = x_n - (h(x_n))/(h'(x_n))

Plot the graph of
$h(x) = x -3\sin(x)$ to get
x_1 --- see attachment for graph

From the attached graph, the first value of x is at 2.2; so:

x_1 = 2.2

So, we have:

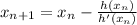
x_(n+1) = x_n - (h(x_n))/(h'(x_n))

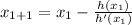
x_(1+1) = x_1 - (h(x_1))/(h'(x_1))

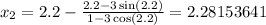
$x_(2) = 2.2 - (2.2 -3\sin(2.2))/(1 -3\cos(2.2)) = 2.28153641$

The process will be repeated until the digit in the 6th decimal place remains unchanged

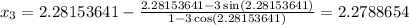
$x_(3) = 2.28153641 - (2.28153641 -3\sin(2.28153641))/(1 -3\cos(2.28153641)) = 2.2788654$

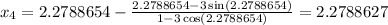
$x_(4) = 2.2788654 - (2.2788654 -3\sin(2.2788654))/(1 -3\cos(2.2788654)) = 2.2788627$

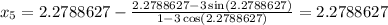
$x_(5) = 2.2788627 - (2.2788627-3\sin(2.2788627))/(1 -3\cos(2.2788627)) = 2.2788627$

Hence:

$x \approx 2.278863$