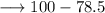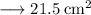Question

21.5 sq. Cm
43 sq. Cm
100 sq. Cm
68.6 sq. Cm

Answer 1

`\large \boxed{ \boxed{ \mathrm{21.5 \: \: cm {}^(2)} }}`

Solution :

By Observing the Above figure, we can conclude that the area of shaded region is equal to the Area of Square minus the sum areas of two equal semicircles (since their diameters are equal)

let's solve for area of square :

`\longrightarrow \: \mathrm{side {}^(2) }`

`\longrightarrow10 {}^(2)`

`\longrightarrow \mathrm{100 \: cm {}^(2) }`

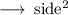
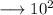
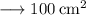
Now,

Radius of the both semicircles measure :

`\longrightarrow (10)/(2)`

`\longrightarrow5 \: cm`

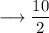
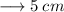
now, let's solve for their area

`\longmapsto 2 * \frac{\pi {r}^(2) }{2}`

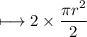
(Since, there are two semicircles)

`\longrightarrow3.14 * 5 * 5`

`\longrightarrow78.5 \: cm {}^(2)`

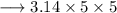
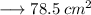
Area of Shaded region = Area of Square - Area of Semicircles, that is

`\longrightarrow100 - 78.5`

`\longrightarrow \mathrm{21.5 \: cm {}^(2) }`

`\large\mathfrak{{\pmb{\underline{\orange{hope \: it \: helps \: you \: }}{\orange{.....}}}}}`